Challenge Question Answers
Answer: Mass Balance in a Chemical Reactor
Given:
k = 0.05 s−1
CA0 = 2 mol/L
CA = 0.2 mol/L (10% of original concentration)
F = 5 L/s
Conversion = 90% (10% excess)
Continuous Stirred Tank Reactor Material Balance:
(F) (CA0) - (F) (CA) = (V) (k) (CA)
V = (F - (CA0 - CA)) / ((k) (CA)
V = (5 (2 - 0.2)) / ((0.05) (0.2))
V = 900L
The minimum reactor volume required to achieve 90% conversion of A is 900L
k = 0.05 s−1
CA0 = 2 mol/L
CA = 0.2 mol/L (10% of original concentration)
F = 5 L/s
Conversion = 90% (10% excess)
Continuous Stirred Tank Reactor Material Balance:
(F) (CA0) - (F) (CA) = (V) (k) (CA)
V = (F - (CA0 - CA)) / ((k) (CA)
V = (5 (2 - 0.2)) / ((0.05) (0.2))
V = 900L
The minimum reactor volume required to achieve 90% conversion of A is 900L
Answer: Engineering Interpolation
- At 110°C and 0.5 MPa =1515.6
- At 110°C and 1 MPa = 1508.8
- At 120°C and 0.5 MPa = 1622.3
- At 120°C and 1 MPa = 1620.9
x1 = 110
x2 = 120
y1 = 0.5
y2 = 1
x = 112
y = 65
The internal energy at 112 degrees Celsius and 0.65 MPa is approximately 1535.2
Answer: Calculus II
Part 1:
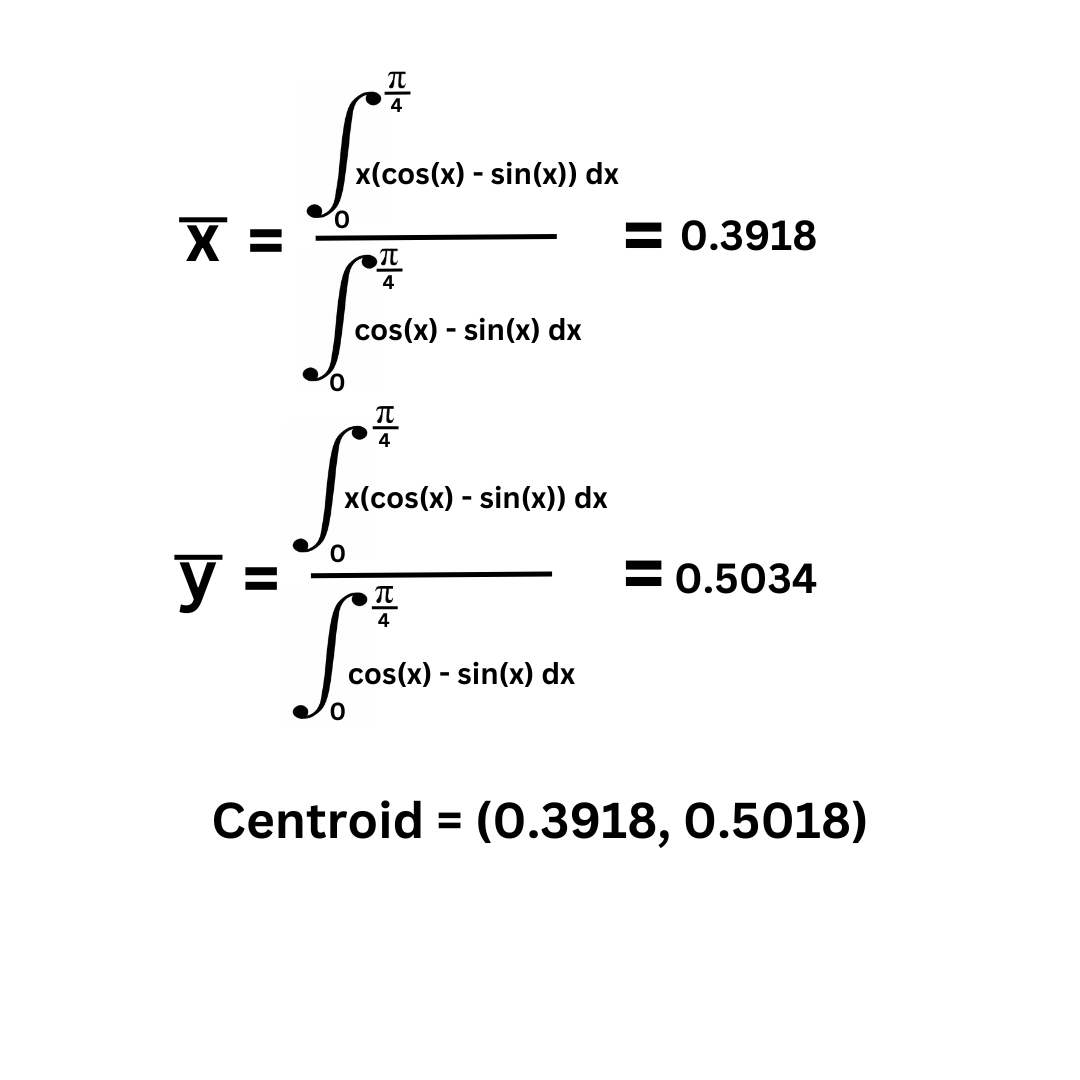
Part 2:
Theorem of Pappus: V = (A) (2pi) (y coordinate of centroid) for volume rotated over the x-axis.
V = 0.779990617 * 2pi * 0.5034033511016
V = 2.4670920233

Part 2:
Theorem of Pappus: V = (A) (2pi) (y coordinate of centroid) for volume rotated over the x-axis.
V = 0.779990617 * 2pi * 0.5034033511016
V = 2.4670920233
Answer: Electronic Structure of Atoms in Chemistry
Part 1:
Change in E = (-2.18 x 10^-18J)((1/n(final)^2) + (1/n(initial)^2))
n(final) = 2
n(initial) = 6
We can us the alternative formula:
1/lambda = (1.097*10^7)((1/n(final)^2) + (1/n(initial)^2))
1/lambda = (1.097*10^7)((1/2^2) + (1/6^2))
1/lambda = 2437777.77778
lambda = 4.1021 * 10^-7 m or 410.21 nm
The wavelength of the electromagnetic radiation emitted from the change in energy state of the electron from n = 6 to n = 2 is 410.21 nm
Part 2: Visible light spectrum
410.21 nm corresponds to violet light
Change in E = (-2.18 x 10^-18J)((1/n(final)^2) + (1/n(initial)^2))
n(final) = 2
n(initial) = 6
We can us the alternative formula:
1/lambda = (1.097*10^7)((1/n(final)^2) + (1/n(initial)^2))
1/lambda = (1.097*10^7)((1/2^2) + (1/6^2))
1/lambda = 2437777.77778
lambda = 4.1021 * 10^-7 m or 410.21 nm
The wavelength of the electromagnetic radiation emitted from the change in energy state of the electron from n = 6 to n = 2 is 410.21 nm
Part 2: Visible light spectrum
410.21 nm corresponds to violet light
Answer: Mass and Energy Balance in Fuel Combustion
Part 1: Air (Nitrogen to Oxygen ratio) = 3.76 moles/N2 per 1 mole/O2
Balanced Reaction:
Chemical + Air(N2 and O2) -> CO2 + H2O + Output Nitrogen (not used in combustion)
Reminder: for every increase in O2's moles by a factor of x, N2 increases in the same factor of x.
C3H8 + (5)O2 + (5*3.76)N2 ->(3)CO2 + (4)H2O + (5*3.76)N2
10% excess: 10% applies to both oxygen and nitrogen
Stoichiometric amounts of O2 and N2:
5.0 * 1.1 = 5.5 moles O2, 5.5 * 3.76 = 20.68 moles N2, so 26.18 moles/Air
Propane (C3H8) Molar mass = 44.097 g/mol
Air MM = 28.9647g/mol
26.18 total moles of Air react with every 1 mole C3H8
26.18mol * 28.9647g/mol = 758.295846g / 1 mole of C3H8
Fuel
(1000g)/(44.097g/mol) = 22.6772796 moles of C3H8
22.6772796 mol/C3H8 * 758.295846g/1mole of C3H8 = 17196.0869 grams of air
Equals 17.1960869 kg/1kg of fuel
Note: You can also apply the 10% excess ratio as a factor of 1.1 at the end of the calculations.
So, the solution is 17.1960869 kilograms of air per kg of fuel with a 10% excess ratio
Part 2:
Balanced Equation:
C3H8 + (5)O2 + (5*3.76)N2 ->(3)CO2 + (4)H2O + (5*3.76)N2
C3H8 + (5)O2 + (18.8)N2 ->(3)CO2 + (4)H2O + (18.8)N2
Enthalpy of combustion = ΔHcomb
At 298 K and 1 atm pressure, ΔHcomb of propane = −2044 kJ/mol of C3H8
Translate units to kJ/kg of C3H8: -2044/44 = -46.45455 * 1000 = -46454.54545 kJ/kg of C3H8
Air is preheated to 400K
Standard enthalpy usually found at 298K, for CO2, O2, N2, H2O
*Include all energy entering the combustion system*
specific heat capacity at a constant pressure (Air) = Cp (Air) = 1.005 KJ/kgK
Q = mcΔT
Q(Air) = 17.1960869kg * 1.005 * (400 - 298)
Q(Air) = 1762.23598 kJ
Adiabatic Flame Temperature:
Total enthalpy released + preheated air = Enthalpy absorbed by the products to reach final temperature
C3H8 + (5)O2 + (18.8)N2 ->(3)CO2 + (4)H2O + (18.8)N2
product mole ratios = 3/25.8, 4/25.8, 18.8/25.8
Cp = CO2 = ~1, H2O = ~1.9, N2 = 1.005 -> Multiply mole ratios by Cp values to find average
Cp avg of products = 1.1432 kJ/kgK
ΔHcomb +Q(Air) = m(products) * Cp(average) * (Tf − 298)
-46454.54545 + 1762.23598 = 18.1960869 * 1.1432 * (Tf − 298)
Tf = 1850.48625 K
Note: Your answer may differ due to rounding during calculations.
Balanced Reaction:
Chemical + Air(N2 and O2) -> CO2 + H2O + Output Nitrogen (not used in combustion)
Reminder: for every increase in O2's moles by a factor of x, N2 increases in the same factor of x.
C3H8 + (5)O2 + (5*3.76)N2 ->(3)CO2 + (4)H2O + (5*3.76)N2
10% excess: 10% applies to both oxygen and nitrogen
Stoichiometric amounts of O2 and N2:
5.0 * 1.1 = 5.5 moles O2, 5.5 * 3.76 = 20.68 moles N2, so 26.18 moles/Air
Propane (C3H8) Molar mass = 44.097 g/mol
Air MM = 28.9647g/mol
26.18 total moles of Air react with every 1 mole C3H8
26.18mol * 28.9647g/mol = 758.295846g / 1 mole of C3H8
Fuel
(1000g)/(44.097g/mol) = 22.6772796 moles of C3H8
22.6772796 mol/C3H8 * 758.295846g/1mole of C3H8 = 17196.0869 grams of air
Equals 17.1960869 kg/1kg of fuel
Note: You can also apply the 10% excess ratio as a factor of 1.1 at the end of the calculations.
So, the solution is 17.1960869 kilograms of air per kg of fuel with a 10% excess ratio
Part 2:
Balanced Equation:
C3H8 + (5)O2 + (5*3.76)N2 ->(3)CO2 + (4)H2O + (5*3.76)N2
C3H8 + (5)O2 + (18.8)N2 ->(3)CO2 + (4)H2O + (18.8)N2
Enthalpy of combustion = ΔHcomb
At 298 K and 1 atm pressure, ΔHcomb of propane = −2044 kJ/mol of C3H8
Translate units to kJ/kg of C3H8: -2044/44 = -46.45455 * 1000 = -46454.54545 kJ/kg of C3H8
Air is preheated to 400K
Standard enthalpy usually found at 298K, for CO2, O2, N2, H2O
*Include all energy entering the combustion system*
specific heat capacity at a constant pressure (Air) = Cp (Air) = 1.005 KJ/kgK
Q = mcΔT
Q(Air) = 17.1960869kg * 1.005 * (400 - 298)
Q(Air) = 1762.23598 kJ
Adiabatic Flame Temperature:
Total enthalpy released + preheated air = Enthalpy absorbed by the products to reach final temperature
C3H8 + (5)O2 + (18.8)N2 ->(3)CO2 + (4)H2O + (18.8)N2
product mole ratios = 3/25.8, 4/25.8, 18.8/25.8
Cp = CO2 = ~1, H2O = ~1.9, N2 = 1.005 -> Multiply mole ratios by Cp values to find average
Cp avg of products = 1.1432 kJ/kgK
ΔHcomb +Q(Air) = m(products) * Cp(average) * (Tf − 298)
-46454.54545 + 1762.23598 = 18.1960869 * 1.1432 * (Tf − 298)
Tf = 1850.48625 K
Note: Your answer may differ due to rounding during calculations.
Answer: First-Order Reaction Kinetics: Concentration of Reactant Over Time
The rate law is given by:
dA/dt = - k[A]
Know:
[A] = concentration of A (mol/L)
k = rate constant (1/s)
t = time (s)
At time t=0, A is [A]0.
Determine the concentration of A at any time t:
dA/dt = - k[A]
Move A to left side and dt to right side:
(1/A) dA = -k dt
Integration:
∫ (1/A) dA = ∫ -k dt
ln[A] = -kt + c
Solve for A:
use e to get A alone:
A = Ce^-kt
C is initial value in the reaction = A0
A = (A0)e^-kt
Therefore, the concentration of A at any time t is:
A(t) = (A0)e^-kt
dA/dt = - k[A]
Know:
[A] = concentration of A (mol/L)
k = rate constant (1/s)
t = time (s)
At time t=0, A is [A]0.
Determine the concentration of A at any time t:
dA/dt = - k[A]
Move A to left side and dt to right side:
(1/A) dA = -k dt
Integration:
∫ (1/A) dA = ∫ -k dt
ln[A] = -kt + c
Solve for A:
use e to get A alone:
A = Ce^-kt
C is initial value in the reaction = A0
A = (A0)e^-kt
Therefore, the concentration of A at any time t is:
A(t) = (A0)e^-kt
Answer - Advanced Thermodynamics
Energy balance at the OFWH:
Assign:
solve for y:
y = (h5 - h4)/(h2 - h4)
Find enthalpy values:
hf is listed in steam tables ->
Find h2 (Enthalpy at 0.7 mPA):
Use:
h5 = hf(0.7 MPa)
h5 = 697.1 kJ/kg
Find y:
y = (h5 - h4)/(h2 - h4)
y = (697.1 - 192.66)/(2812.2 - 192.66)
y = 0.1926 -> 19.26% (approximately)
(Results may vary slightly due to interpolation and steam table values, but the exact answer will be close to the given approximate value)
Assign:
- h2 = Enthalpy of steam at 0.7 MPa
- h4 = Enthalpy of compressed liquid from Pump 1
- h5 = Enthalpy of saturated liquid at 0.7 MPa
solve for y:
y = (h5 - h4)/(h2 - h4)
Find enthalpy values:
hf is listed in steam tables ->
- At 10 kPa (condenser pressure): hf = 191.81 kJ/kg
- At 0.7 MPa (feedwater heater pressure): hf = 697.1 kJ/kg
Find h2 (Enthalpy at 0.7 mPA):
Use:
- ηT=85%
- h2s = hg + ((s1 - sg)/(ssup - sg)
- h2 = h1 − ηT(h1 − h2s)
- hg = 2762.5
- sg = 6.8625
h2s = hg + ((s1 - sg)/(ssup - sg)
h2s = 2762.5 + ((6.6583 - 6.8625)/(7 - 6.8625)) x (2800 - 2762.5)
h2s = 2706.86
h2 = h1 − ηT(h1 − h2s)
h2 = 3410.2 − 0.85(3410.2 − 2706.86)
h2 = 2812.2 kJ/kg
Find h4 (Enthalpy after post 1): - vf = 0.001043 m³/kg
- wp = vf(P5 - P4)/ηp
- h4 = h3 + wp
h3 = hf(10 kPa)
h3 = 191.81 kJ/kg
wp = vf(P5 - P4)/ηp
wp = 0.7207/0.85 = 0.847
h4 = h3 + wp
h4 = 191.84 + 0.847
h4 = 192.66 kJ/kg
h5 = hf(0.7 MPa)
h5 = 697.1 kJ/kg
Find y:
y = (h5 - h4)/(h2 - h4)
y = (697.1 - 192.66)/(2812.2 - 192.66)
y = 0.1926 -> 19.26% (approximately)
(Results may vary slightly due to interpolation and steam table values, but the exact answer will be close to the given approximate value)